Ромб стоїть перед нами як геометрична фігура з рівними сторонами, де кожна грань шепоче про симетрію, а діагоналі перетинаються під прямим кутом, ніби створюючи хрест долі. Ця форма з’являється в архітектурних шедеврах, ювелірних прикрасах і навіть у повсякденних об’єктах, як плитка на підлозі, де точне обчислення площі може врятувати від зайвих витрат матеріалу. Коли ви беретеся за розрахунок, то ніби розкриваєте таємницю, яка ховається в простих лініях, перетворюючи абстрактні числа на реальну користь.
Уявіть, як ромб оживає в руках архітектора, що проектує дах будівлі, або в руках школяра, який намагається розв’язати задачу з геометрії. Площа тут не просто число – це ключ до розуміння простору, де помилка в розрахунку може призвести до хаосу в конструкції. А тепер перейдімо до суті, розкриваючи крок за кроком, як саме знайти цю площу, спираючись на перевірені методи.
Визначення ромба та його ключові властивості
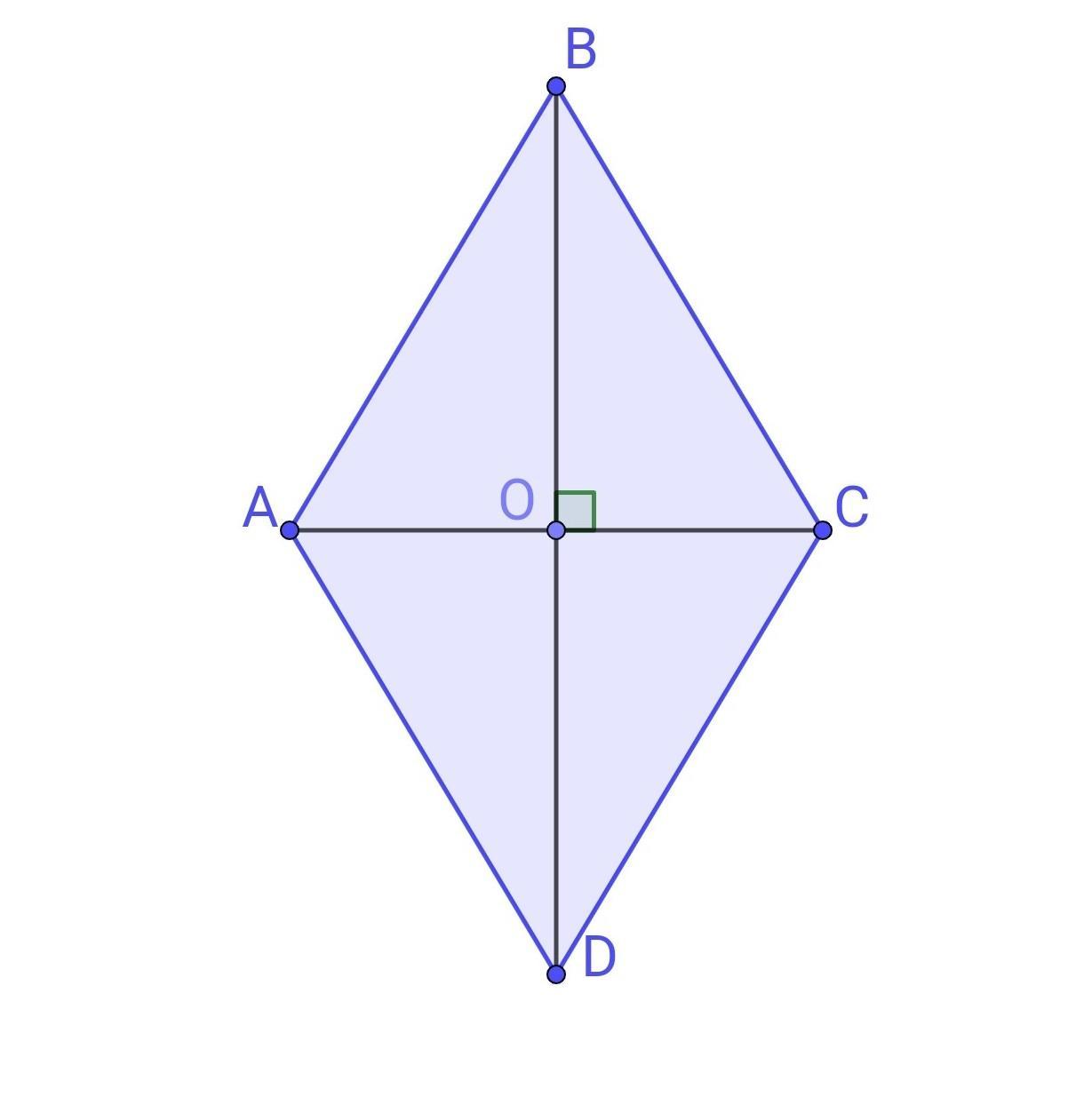
Ромб – це чотирикутник, де всі сторони рівні за довжиною, а протилежні кути рівні між собою, з діагоналями, що перетинаються перпендикулярно і ділять одна одну навпіл. Ця фігура, подібна до скошеного квадрата, володіє унікальною симетрією, де кожна діагональ стає віссю, що розрізає ромб на два рівних трикутники. Властивості ромба роблять його ідеальним для обчислень, бо вони спрощують формули, перетворюючи складні задачі на елегантні рівняння.
Одна з найцікавіших рис – те, що ромб є паралелограмом, але з додатковою умовою рівності сторін, що додає йому стабільності в геометричних побудовах. Кути ромба завжди попарно гострі та тупі, якщо це не квадрат, і це впливає на розрахунок площі, особливо коли ми звертаємося до тригонометричних функцій. Зрозумівши ці основи, ви відчуєте, як ромб стає не просто фігурою на папері, а інструментом для реальних застосувань, від дизайну до інженерії.
Історично ромб відомий ще з часів давньогрецьких математиків, як Евклід, який описував його властивості в своїх “Елементах”, підкреслюючи роль діагоналей у поділі фігури. Сьогодні, у 2025 році, ці знання еволюціонували, інтегруючись у комп’ютерне моделювання, де ромби формують сітки в 3D-графіці. Така глибина робить ромб не просто об’єктом вивчення, а живою частиною сучасної науки.
Основні методи обчислення площі ромба
Обчислення площі ромба можна порівняти з розкриттям шаруватого пирога, де кожен шар – це інший метод, від простого множення до тригонометрії. Найпоширеніший підхід базується на відомих параметрах, як довжина сторони чи діагоналей, дозволяючи адаптувати розрахунок до доступних даних. Ці методи не тільки точні, але й гнучкі, роблячи геометрію доступною для всіх, від новачків до експертів.
Кожен метод має свої нюанси: наприклад, коли діагоналі відомі, розрахунок стає швидким, ніби удар блискавки, а от з висотою доводиться трохи поміркувати. Важливо пам’ятати, що ромб – це завжди плоска фігура, тому площу ми вимірюємо в квадратних одиницях, чи то сантиметри, чи метри. Давайте розберемо ці методи детально, з формулами, що витримали перевірку часом.
Метод через діагоналі
Діагоналі ромба – це його серце, бо вони перетинаються під прямим кутом і ділять фігуру на чотири прямокутні трикутники. Формула площі тут проста: S = (d₁ × d₂) / 2, де d₁ і d₂ – довжини діагоналей. Цей спосіб блискавичний, бо не вимагає знання кутів чи висоти, роблячи його ідеальним для швидких розрахунків.
Чому це працює? Кожна діагональ ділить ромб на два рівнобедрених трикутники, а їхня площа обчислюється як половина добутку основи та висоти, що в сумі дає загальну формулу. У 2025 році цей метод часто застосовують у програмному забезпеченні для дизайну, де алгоритми автоматично обчислюють площу за сканованими діагоналями. За даними сайту onlinemschool.com, ця формула є однією з найнадійніших, підтвердженою тисячами прикладів.
Метод через сторону та висоту
Якщо ви знаєте довжину сторони ромба (a) і висоту (h), площа стає продуктом цих величин: S = a × h. Висота тут – це перпендикулярна відстань між протилежними сторонами, ніби невидима опора, що тримає форму. Цей метод нагадує обчислення площі паралелограма, але з акцентом на рівність сторін.
Щоб знайти висоту, якщо її немає, можна скористатися тригонометрією: h = a × sin(α), де α – кут ромба. Це додає шар глибини, особливо коли ромб скошений, і робить розрахунок більш універсальним. Практики в будівництві часто обирають цей метод, бо висоту легко виміряти на місцевості.
Метод через сторону та кут
Тригонометрія вривається в обчислення з формулою S = a² × sin(α), де a – сторона, а α – один з кутів. Цей підхід оживає, коли кути відомі, перетворюючи ромб на поле для синусів і косинусів. Синус кута тут діє як множник, що враховує нахил фігури.
Для гострого кута sin(α) дає точне значення, а для тупого – використовуйте протилежний. Цей метод особливо корисний у фізиці, де ромби моделюють сили в механіці. Згідно з матеріалами з сайту libretexts.org, ця формула походить від властивостей паралелограмів і перевірена в численних наукових працях.
Покрокові приклади обчислення площі
Перейдімо до практики, де теорія набуває форми чисел, ніби фарби на полотні. Ось кілька прикладів, що ілюструють різні методи, з детальними кроками для ясності. Кожен приклад базується на реальних сценаріях, щоб ви могли застосувати знання на ділі.
- Приклад з діагоналями: Уявіть ромб з діагоналями 10 см і 24 см. Крок 1: Помножте діагоналі – 10 × 24 = 240. Крок 2: Поділіть на 2 – 240 / 2 = 120 см². Це площа, ідеальна для розрахунку плитки в ромбоподібній кімнаті.
- Приклад з стороною та висотою: Сторона 5 см, висота 4 см. Просто множимо: 5 × 4 = 20 см². Якщо висоти немає, виміряйте перпендикуляр між сторонами – це додасть точності в будівництві.
- Приклад з стороною та кутом: Сторона 7 см, кут 60°. Sin(60°) = √3/2 ≈ 0.866. Тоді S = 7² × 0.866 ≈ 49 × 0.866 ≈ 42.43 см². Цей метод блискучий для скошених форм у дизайні.
- Складний приклад: Діагоналі 8 см і 6 см, але перевірте, чи це ромб (діагоналі перпендикулярні). S = (8 × 6)/2 = 24 см². Додайте перевірку: довжина сторони = √((4)^2 + (3)^2) = 5 см для кожної.
Ці приклади показують, як методи переплітаються, дозволяючи адаптувати розрахунок до ситуації. У реальному житті, наприклад, у 2025 році, архітектори використовують додатки для сканування форм, але базові кроки залишаються незмінними, додаючи впевненості в результатах.
Застосування площі ромба в реальному житті
Площа ромба не ховається в підручниках – вона виривається в світ, формуючи дахи будинків, де точний розрахунок економить матеріали, або в ювелірці, де ромбоподібні діаманти оцінюють за площею поверхні. У природі ромби з’являються в кристалах солі, де обчислення допомагає хімікам моделювати структури. А в мистецтві, як у творах Ешера, ромби створюють оптичні ілюзії, де площа стає частиною візуальної магії.
У сучасній техніці, станом на 2025 рік, ромби інтегрують у сонячні панелі з ромбоподібними клітинками, де площа визначає ефективність енергії. Це робить геометрію не абстракцією, а інструментом прогресу, де кожен розрахунок – крок до інновацій.
Навіть у спорті, як у бейсболі, поле має ромбоподібну форму, і обчислення площі допомагає в плануванні стадіонів. Така універсальність робить тему живою, спонукаючи до експериментів з власними проектами.
Типові помилки при обчисленні площі ромба
- 😕 Змішування діагоналей з сторонами: Багато хто плутає d₁ з a, що призводить до помилок; завжди перевіряйте, чи діагоналі перпендикулярні.
- 🤔 Ігнорування кута в тригонометричній формулі: Використання cos замість sin може спотворити результат; пам’ятайте, sin для висоти.
- 😤 Неправильне ділення навпіл: У формулі з діагоналями забувають /2, подвоюючи площу; це класична пастка для поспіху.
- 🙄 Застосування формули квадрата до ромба: Якщо кути не 90°, S ≠ a²; завжди враховуйте кут.
- 😩 Помилки в одиницях: Змішування см і м призводить до гігантських або крихітних значень; уніфікуйте міри.
Уникаючи цих помилок, ви перетворите обчислення на точну науку, додаючи впевненості в кожному кроці.
Розширені методи для просунутих користувачів
Для тих, хто заглиблюється далі, ромб відкриває двері до векторної геометрії, де площа = |вектор AB × вектор AD|, використовуючи векторний добуток. Це метод для 3D-моделей, де ромб стає частиною складних поверхонь. У координатній площині, з вершинами в точках, площа обчислюється через детермінант матриці координат, додаючи математичної елегантності.
У калькулюсі ромб може бути інтегрований для обчислення площі під кривими, але базово це зводиться до тих же формул. Просунуті користувачі в 2025 році використовують AI для оптимізації, але розуміння основ залишається ключем. Це ніби перехід від велосипеда до автомобіля – швидше, але фундамент той самий.
Експериментуйте з програмуванням: напишіть скрипт на Python, де вводите параметри, і отримуєте площу. Такий підхід робить геометрію інтерактивною, перетворюючи теорію на цифрову реальність.
Інструменти та ресурси для обчислення
У цифрову еру інструменти полегшують життя: онлайн-калькулятори на сайтах як mathros.net.ua дозволяють ввести дані й отримати результат миттєво. Мобільні додатки, як GeoGebra, візуалізують ромб, показуючи динамічні зміни площі при зміні параметрів.
Для глибшого вивчення книги як “Елементи” Евкліда або сучасні посібники з геометрії пропонують теоретичну базу. У 2025 році VR-симуляції дозволяють “прогулятися” всередині ромба, обчислюючи площу в реальному часі. Ці ресурси роблять навчання захопливим, ніби пригода в світі форм.
| Метод | Формула | Переваги | Недоліки |
|---|---|---|---|
| Через діагоналі | S = (d₁ × d₂) / 2 | Швидкий, не потребує кутів | Потрібні обидві діагоналі |
| Через сторону та висоту | S = a × h | Простота вимірювання | Висота не завжди очевидна |
| Через сторону та кут | S = a² × sin(α) | Гнучкий для скошених форм | Вимагає тригонометрії |
Ця таблиця ілюструє порівняння методів, допомагаючи обрати оптимальний залежно від даних. Джерело: матеріали з сайтів mathros.net.ua та onlinemschool.com.
З такими інструментами обчислення стає не тягарем, а задоволенням, відкриваючи нові горизонти в геометрії. Продовжуйте експериментувати, і ромб розкриє ще більше секретів.






